Änderungen und Erweiterungen vom 5.5.2022

1. Bootstrap der Faktorenanalyse
   Das Bootstrap-Verfahren kann nun auch auf die Faktorenanalyse angewendet werden.
    Damit kann jetzt für die Faktorenzahl und für jede einzelne Faktorladung deren
    (1) Standardfehler, (2) p-Wert und  (3) Konfidenzintervall ermittelt werden, was seither
    im Standardmodell der Faktorenanalyse nicht möglich war.
    Almo liefert beispieslweise folgende (stark gekürzte) Ausgabe für den Bootstrap der Eigenwerte
    und der Faktorladungen aus einer 6*6-Korrelationsmatrix:

                 ┌────────────┬─────────────────────────────────────────────────┐

                 │ Original-  │           Bootstraps der Eigenwerte             │

                 │ Stichprobe │   Ergebnisse aus  1000 Bootstrapstichproben     │

                 │            │                                                 │

                 │            │Mitt.wert│Standard │Signifik.│ Konfidenzintervall│

                 │ Eigenwert  │Eigenwert│  fehler │    p    │   unten     oben  │

                 ├────────────┼─────────┼─────────┼─────────┼─────────┼─────────┤

    Eigenwert  1        2.5909    2.6035    0.0928    0.0010    2.4396    2.7970

    Eigenwert  2        1.5778    1.5729    0.0899    0.0010    1.3852    1.7331

    Eigenwert  3        0.6967    0.7052    0.0489    0.9990    0.6159    0.7971

    Eigenwert  4        0.5819    0.5735    0.0412    0.9990    0.4908    0.6536

    Eigenwert  5        0.2950    0.2991    0.0273    0.9990    0.2490    0.3569

    Eigenwert  6        0.2577    0.2459    0.0219    0.9990    0.2044    0.2901

Die p-Werte für den 1. und 2. Eigenwert sagen aus, dass diese beiden signifikant größergleich 1.0 sind,
d.h. dem "Kaiser-Kriterium" entsprechen. Wichtig wird diese Information, wenn ein Eigenwert
knapp über oder unter 1.0 liegt.

                    ┌────────────┬─────────────────────────────────────────────────┐

                    │Original-   │          Bootstrap der Faktorladungen           │

                    │Stichprobe  │            Ergebnisse aus Bootstrap             │

                    │            │                                                 │

                    │rotierte    │   Standard │ Signifikanz│    Konfidenzintervall │

                    │Faktorladung│     fehler │      p-Wert│   unten         oben  │

    ────────────────┼────────────┼────────────┼────────────┼───────────────────────┤

    Faktor 1  V1        0.8925       0.0122       0.0010       0.8657       0.9126

              V2        0.9111       0.0092       0.0010       0.8908       0.9275

              V3        0.8892       0.0112       0.0010       0.8640       0.9085

              V4        0.1664       0.0482       0.0020       0.0748       0.2638

              V5        0.0540       0.0599       0.3420      -0.1751       0.0576

              V6        0.0979       0.0609       0.1220      -0.0268       0.2188

    ───────────────────────────────────────────────────────────────────────────────

    Faktor 2  V1        0.2121       0.0337       0.0010      -0.1877      -0.0561

              V2        0.3246       0.0406       0.8740      -0.0874       0.0726

              V3        0.2444       0.0386       0.0200      -0.1575      -0.0114

              V4       -0.6527       0.0288       0.0010      -0.8152      -0.7036

              V5       -0.7418       0.0243       0.0010      -0.8166      -0.7234

              V6       -0.6257       0.0413       0.0010      -0.7774      -0.6205

Der p-Wert von V1 (in Faktor 1) von 0.001 sagt aus, dass der Forscher mit 1-p = 0.999 sicher sein kann,
dass die Faktorladung von 0.8925 von .0 verschieden ist - genauer formuliert, dass er sich nur mit p=0.001
irrt, wenn er annimmt, dass die Faktorladung von V1 ungleich .0 ist. So erweist es sich in unserem
Beispiel, dass V1 und 3 auch noch schwach aber signifikant auf dem 2. Faktor laden.
Wahlweise können anstelle der Faktorladungen auch die Faktorwertkoeffizienten dem Bootstrap-
Verfahren unterworfen werden

2. Handbuch zum Bootstrap bei Faktorenanalyse
Im Handbuch wird in 55 Seiten das Bootstrap-Verfahren und die besondere Vorgehensweise beim
Bootstrapping der Faktorenanalyse  beschrieben. Siehe hier

 Hier ist das Inhaltsverzeichnis

P30.6.1 Vorgehensweise beim Bootstrap

   P30.6.1.1  Standardfehler

   P30.6.1.2  Konfidenzintervall,  Perzentil-Verfahren

   P30.6.1.3  Signifikanz, p-Wert

   P30.6.1.4  Mittelwert und Verzerrung

   P30.6.1.5  Der Forschungsbericht

   P30.6.1.6  Die Zahl der Bootstrap-Stichproben

   P30.6.1.7 Daten lesen und verarbeiten beim Bootstrap

 

P30.6.2 Vorgehensweise beim Bootstrap der Faktorenanalyse

   P30.6.2.0  Sonderfall: Faktorenanalyse mit 1 Faktor

   P30.6.2.1  Bootstrap der Eigenwerte

   P30.6.2.2  Unsere Beispieldaten:  Die Holzinger-Swineford-Daten

   P30.6.2.3  Rotation und "gemeinsamer Faktoren-Raum"

   P30.6.2.4  Zielmatrix mit rechtwinkligen Koordinatenachsen

   P30.6.2.5  Zielmatrix mit schiefwinkligen Koordinatenachsen

   P30.6.2.6  Die gesamte Varimax- bzw. Quartimin-Faktorladungsmatrix als

              Zielmatrix

 

P30.6.3  Bootstrap-Programm Prog30ml.Msk

   P30.6.3.1  Zu faktorisierende Variable

   P30.6.3.2  Spezielle Kein-Wert-Behandlung

   P30.6.3.3  Optionen für Faktorenanalyse

   P30.6.3.4  Faktorenanalytisches Modell und Eigenwert-Verfahren

   P30.6.3.5  Faktorenzahl und Kommunalitätenschätzung

   P30.6.3.6  Distanzmatrix ermitteln und Zwischenergebnisse ausgeben

   P30.6.3.7  Die Bootstrap-Optionsbox

 

P30.6.4  Bootstrap-Ergebnisse aus Programm Prog30ml.Msk

   P30.6.4.1  Ergebnisse aus Bootstrap bei rechtwinkliger Zielmatrix

   P30.6.4.2  Ergebnisse aus Bootstrap bei schiefwinkliger Zielmatrix

   P30.6.4.3  Ergebnisse aus Bootstrap bei Faktorenanalyse mit 1 Faktor

 

Anhang: Vergleich der Studie von Zientek & Thompson (2007) mit Almo

Literatur zu Bootstrap

 

3. Bootstrap der Randmittel beim ALM
Beim ALM werden nun auch die Randmittel dem Bootstrapping unterzogen.
Ermittelt werden (1) Standardfehler und (2) das Konfidenzintervall.
Das Handbuch zum Bootstrap des ALM und auch das Bootstrap-Programm selbst
wurden etwas überarbeitet.
Anhand eines Beispiels wurde ein ausführlicher Vergleich mit dem SPSS-ALM-Bootstrap
gerechnet, der im überarbeiteten Handbuch auch beschrieben wird.

 

 

Änderungen und Erweiterungen vom 4.10.2021
1. Das Bootstrap-Verfahren kann nun auch auf die Logit- und Probitanalyse angewendet werden
    Das gilt für folgende Koeffizienten
    a.  Die Regressionskoeffizienten der unabhängigen quantitativen Variablen
    b.  Die Regressionskoeffizienten der Dummies der unabhängigen nominalen Variablen
    c.  Die paarweisen Vergleiche (Kontraste) der Dummies der jeweiligen unabhängigen
         nominalen Variablen
    d.  Die Risikokoeffizienten exp(ß) aller unabhängigen Variablen alternativ zu den Regressions-
         koeffizienten. Nicht bei der Probitanalyse möglich.

     Für diese Koeffizienten werden der Standardfehler, die Signifikanz p und das Konfidenzintervall
     durch Bootstrap ermittelt.

2.  Die spezielle Programm-Maske "Prog22m5" für eine besonders einfache Dateneingabe
    wurde entwickelt

3.  Es wurde das Handbuch "Bootstrap bei Logit-und Probitanalyse" verfasst.
     Das Verfahren wird darin ausführlich beschrieben, die Eingabe in die spezielle
     Programm-Maske Prog22m5 erklärt und die Bootstrap-Ergebnisse erläutert.

Folgende spezielle Programm-Masken für das Bootstrap-Verfahren sind nunmehr verfügbar
Prog05m6: Basis-Statistiken mit Bootstrap
                  Mittelwert, Standardabweichung                                                                              
                  Median, Quartile, Konfidenzintervall etc.

Prog05m7: Häufigkeitsverteilung, Anteilswerte mit Bootstrap

Prog19em: Korrelationsmatrix für quantitative, ordinale und nominale Variable                                                  

                   auch Matrix von beliebig wählbaren Partialkorrelationen

                   mit Bootstrap

Prog20my: Allgemeines Lineares Modell mit Bootstrap                                                                              

Prog22m5: Logit- und Probit-Analyse mit Bootstrap

In diesen Programmen wird durch Bootstrap der Standardfehler, die Signifikanz p
und das Konfidenzintervall für den jeweiligen Koeffizienten ermittelt

13.6.2021 Bootstrap 
In Almo kann gegenwärtig das Bootstrap-Verfahren eingesetzt werden für

              1. die Basisstatistiken mit Programm-Maske Prog05m6

              2. die Korrelationsmatrix (inkl. Partialmatrix) mit Programm-Maske Prog19em

              3. das Allgemeine Lineare Modell (ALM) mit Programm-Maske Prog20my

 

Für das Bootstrap-Verfahren, insbesondere für das Bootstrap beim ALM wurde ein ausführliches
Handbuch verfasst.

           Almo-Dokument 13b "Bootstrap beim Allgemeinen Linearen Modell" (hier).

 

Es ist beabsichtigt weitere in Almo vorhandene statistische Methoden durch Bootstrap zu erweitern.

Ein erster Blick auf das Bootstrap-Verfahren.

Aus einer vorliegenden Stichprobe (wir nennen sie "originale" Stichprobe) der Größe n werden

zufällig n Datensätze mit Zurücklegen ausgewählt. Dadurch entsteht die Bootstrap-Stichprobe Nr. 1.

Originalstichprobe und Bootstrapstichprobe sind also gleich groß. Das Zurücklegen allerdings

bewirkt, dass manche Datensätze mehrfach ausgewählt werden und dass manche Datensätze

der originalen Stichprobe nicht in die Bootstrap-Stichprobe geraten. Auf diese Weise werden viele,

etwa 1000 Bootstrap-Stichproben erzeugt.

 

Betrachten wir ein Beipiel, bei dem 1000 Stichproben aus der Orirginal-Stichprobe gezogen

werden. Für die originale Stichprobe und für alle 1000 Bootstrap-Stichproben

rechnet Almo ein ALM. Die Ergebnisse des ALM für die Original-Stichprobe werden

zuerst ausgegeben. Die Ergebnisse aus den 1000 Bootstrapstichproben werden zusammen-

gefasst, im einfachsten Fall nur gemittelt und dann separat ausgegeben. Besonders bedeutsam

ist, dass aus dem Bootstrapping empirische Verteilungen für die verschiedenen Koeffizienten

des ALM gewonnen werden. Dadurch ist es möglich, Standardfehler, Signifikanzen (p-Werte) und

Konfidenzintervalle, für die keine Verteilungsannahmen erforderlich sind, für die verschiedenen

Koeffizienten des ALM zu ermitteln.

Das ist der primäre Zweck des Bootstrap-Verfahrens. Es erzeugt "verteilungsfreie" Schätzer.

 

Betrachten wir als Beispiel den Regressionskoeffizienten b1 für eine Kovariate x1. Aus den

1000 Bootstrapstichproben erhalten wir 1000 Werte für b1. Wir berechnen deren Mittelwert

und ihre Standardabweichung. Die Standardabweichung ist dann der "Standardfehler" von b1.

 

 Die obere und untere Grenze des Konfidenzintervalls für beispielsweise ein Konfidenzniveau

 von 95% erhalten wir sehr einfach in folgender Weise: Die 1000 b1-Werte werden der Größe

 nach (aufsteigend) sortiert. Vom maximalen b1-Wert werden absteigend 2,5% von 1000 also

25 Werte heruntergezählt. Der dort in Position 975 stehende b1-Wert ist die obere Intervallgrenze.

 Entsprechend wird vom minimalen Wert ausgehend 25 Werte hinaufgezählt. So wird in Position 26

der untere Grenzwert gefunden. Zwischen den beiden Grenzwerten befinden sich dann 95% aller Werte

und außerhalb der Grenzwerte 5% aller Werte. Diese sehr einfache Berechnungsweise wird als

 "Perzentil-Verfahren" bezeichnet. Almo verwendet dieses Verfahren und optional das etwas

komplexere Perzentil-t -Verfahren.

 

Ob ein Koeffizient zweiseitig signifikant ist, wird zunächst daran erkannt, ob das für ihn

festgestellte Konfidenzintervall bei dem vom Forscher geforderten Konfidenzniveau (z.B. von  95%)

den Wert 0 einschließt. Ist das nicht der Fall, dann ist der Koeffizient signifikant. Soll umgekehrt die

Signifikanz als exakter p-Wert ermittelt werden, dann geht es darum, dasjenige Konfidenzniveau

zu finden, das ein Konfidenzintervall erzeugt, das gerade noch den Wert 0 unter- oder oberhalb seiner

Grenzen positioniert. 1.0 minus diesem Konfidenzniveau/100 ist dann die Signifikanz p.

Beim Perzentil-t -Verfahren ist die Berechnung des p-Wertes etwas komplexer.

 

Als bester Schätzer für b1 wird der Wert aus der Original-Stichprobe und nicht der

Mittelwert aus den Bootstrapstichproben für den Forschungsbericht verwendet.

Als seinen Standardfehler wird die aus dem Bootstrap gewonnene Standardabweichung

eingesetzt, als seine Signifikanz p und sein Konfidenzintervall werden die aus

dem Perzentil-Verfahren errechneten Werte eingesetzt. Alle diese Koeffizienten sind

"verteilungsfrei". Auf diese Weise lassen sich viele Koeffizienten aus den verschiedenen

statistischen Verfahren behandeln. Bootstrap liefert für diese Koeffizienten den Standardfehler,

die Signifikanz (p-Wert) und das Konfidenzintervall, wobei diese drei "verteilungsfrei" sind.

 

Bootstrap bei Basisstatistiken

Almo führt für diese Koeffizienten ein Bootstrap-Verfahren durch
   1. für ordinale Variable
      1.1. 1. und 3. Quartil
      1.2. Median
   2. für quantitative Variable
      2.1. arithmetsches Mittel
Für diese Koeffizienten werden durch Bootstrap errechnet
      a. der Mittelwert aus allen Bootstrap-Stichproben
   b. der Standardfehler als Standardabweichung aus allen Bootstrap-Stichproben
   c. das Konfidenzintervall durch das Perzentil-Verfahren

 

Bootstrap bei Allgemeinem Linearen Modell (ALM)

Almo führt für diese Koeffizienten ein Bootstrap-Verfahren durch

   1. für die Kovariaten:

      1.1. die Regressionskoeffizienten

      1.2. die Eta-Korrelationen

   2. für die nominalen Variablen:

      2.1. die Effekte der Haupt-und Interaktions-Dummies

      2.2. die Eta-Korrelationen der Haupt-und Interaktions-Dummies

      2.3. die partielle multiple Eta-Korrelation aus den Dummies je
           nominale Variable

      2.4. die paarweisen Mittelwertsvergleiche innerhalb der nominalen
           Variablen

   3. für die Konstante:

      3.1. den Regressionskoeffizienten

   4. für alle unabhängigen Variablen zusammen:

      4.1. die multiple Korrelation

 
Für alle diese Koeffizienten werden durch Bootstrap errechnet
      a. der Mittelwert aus allen Bootstrap-Stichproben
   b. der Standardfehler als Standardabweichung aus allen Bootstrap-Stichproben
   c. die Signifikanz (p-Wert) durch das einfache Perzentilverfahren oder
      das Perzentil-t –Verfahren  
   d. das Konfidenzintervall durch das einfache Perzentilverfahren oder das
      Perzentil-t -Verfahren

            Das Konfidenzniveau für das zu ermittelnde Intervall ist beliebig wählbar. Üblich ist
            95.00. Damit wird überprüft, ob der jeweilige Koeffizient mindestens auf dem Niveau
            p=0.05 signifikant ist. 

Im multivariaten Fall wenn zwei oder mehrere abhängige Variable vorhanden sind,
werden folgende Koeffizienten als Mittelwert aus allen Bootstrapstichproben berechnet
      1. für die Kovariaten:
      1.1. Wilks lambda bzw. Pillais Spur
      1.2. die Korrelation nach Pillai
   2. für die nominalen Variablen:
      2.1. Wilks lambda bzw. Pillais Spur je Haupt-und Interaktions-Dummies
      2.2. die Korrelation nach Pillai je Haupt-und Interaktions-Dummy
      2.3. die partielle multiple Pillai-Korrelation aus den Dummies je
           nominale Variable
   3. für alle unabhängigen Variablen zusammen:
      3.1. Pillais Spur
      4.1. die multiple Korrelation nach Pillai
Für diese Koeffizienten aus der multivariaten Analyse werden die oben unter a, b, c und d
durch Bootstrap errechnete Maßzahlen errechnet, das sind Bootstrap-Mittelwert, Standard-
fehler, p-Wert, Konfidenzintervall.

 
Bootstrap bei Korrelationsmatrix
Almo führt für den Korrelationskoeffizienten ein Bootstrap-Verfahren durch. 
Abhängig vom Messniveau der Variablen können das folgende Korrelationskoeffizienten sein

 

                                         nominal-        nominal-  

                   quant.   ordinal      dichotom        polytom   

                  +--------------------------------------------------+

     quantitativ  ¦   r* ¦Groß-Gamma ¦punktbiserial r ¦     Eta      ¦

                  +------+-----------+----------------+--------------¦

         ordinal  ¦      ¦  tau-b    ¦biserial. tau-b ¦  Groß-Gamma  ¦

                  +------+-----------+----------------+--------------¦

nominal-dichotom  ¦      ¦           ¦      Phi       ¦     Phi'     ¦

                  +------+-----------+----------------+--------------¦

 nominal-polytom  ¦      ¦           ¦                ¦   Cramers V  ¦

                  +--------------------------------------------------+

 r* = Produkt-Moment-Korrelation

 

Zum Gross-Gamma-Kalkül und -Koeffizienten siehe Almo-Dokument Nr. 5 "Korrelation",
besonders Abschnitt P19.0.3. (hier)
Sind nominal-polytome Variable vorhanden, dann werden diese zuerst in Dummies aufgelöst.
Durch eine kanonische Korrelation werden sie dann wieder zusammengefasst
und in einer 2. Korrelationsmatrix ausgegeben.

Alle Korrelationskoeffizienten r(ik) sind "proportional reduction of error"-Koeffizienten.
Werden sie quadriert, dann drücken sie den Anteil aus, um den sich die Fehlerstreuung in
der Variablen k reduziert, wenn i als erklärende Variable eingeführt wird.
In der Programm-Maske Prog19em für das Bootstrapping kann durch eine Option
aus der Korrelationsmatrix eine partielle Korrelationsmatrix abgeleitet werden.
Für sie gelten die folgenden Angabe in der selben Weise.

Für den (jeweiligen) Korrelationskoeffizienten werden durch Bootstrap errechnet 

      a. der Mittelwert aus allen Bootstrap-Stichproben
   b. der Standardfehler

      als Standardabweichung aus allen Bootstrap-Stichproben
   c. die Signifikanz (p-Wert) durch das einfache Perzentilverfahren oder
      das Perzentil-t –Verfahren

   d. das Konfidenzintervall durch das einfache Perzentilverfahren oder das
      Perzentil-t -Verfahren

Das Konfidenzniveau für das zu ermittelnde Intervall ist beliebig wählbar.

 

 

13.7.2020    Die Programme zur Daten-Imputation und das Handbuch dazu wurden grundlegend
                     überarbeitet
                     a. Das neue Handbuch trägt jetzt den Titel Daten-Imputation und "plausible values"
                     b. Es wurden neue Programme hinzugefügt bzw. bestehende Programme erweitert,
                         die für fehlende Werte Ersatzwerte generieren und dabei (1) das ALM, (2) das ALM mit
                         vorausgehender Hauptkomponenten-Zerlegung, (3) die Logitanalyse und (4) die Cluster-
                         analyse einsetzen.
                     c. Hinzugefügt wurden Programm zur Erzeugung von multipel imputierten Variablen und
                         plausible values. Im Handbuch wurde ein entsprechendes Kapitel hinzugefügt.

                     Almo enthält jetzt folgende 8 Programm-Masken zur Daten-Imputation

                        ALM-          HALM-          Logit-         Cluster-

                        Imputation    Imputation*    Imputation     Imputation

┌────────────────────┬─────────────┬──────────────┬──────────────┬──────────────┐

│Ein-Wert-Imputation │ Prog45mm_fw │ Prog45Hk_fw  │   Prog45mz   │ ProgImp_Clust│

│                    │             │              │              │              │

│multiple Imputation │ Prog45mm_Imp│ Prog45Hk_Imp │              │              │

│                    │             │              │              │              │

│plausible values    │ Prog45mm_PV │ Prog45Hk_PV  │              │              │

│Imputation          │             │              │              │              │

└────────────────────┴─────────────┴──────────────┴──────────────┴──────────────┘
* HALM-Imputation = Imputation durch ALM mit vorausgehender Hauptkomponenten-Zerlegung

                     Programm Prog20mo zum ALM wurde so erweitert, dass es Daten, die multipel
                     imputierte Variable oder "plausible values" enthalten, auswerten kann.

 

Die fortlaufende Durchnummerierung der Almo-Versionen haben wir 2012 mit der Nummer 15 beendet.
Almo existiert seit vielen Jahren und wird auch noch viele weitere Jahre gepflegt und erweitert werden
- wobei wir jeweils umfangreichere Änderungen dokumentieren werden.

  

 6.2.2019  Für das Allgemeine Lineare Modell wurden Programm und Handbuch Teil I (Dokument
                    Nr. 13) überarbeitet.
                     Programm:
                     a. Für die Schätzverfahren der fitting constants I und II (SS-Typ II) und das sequentielle
                         Verfahren (SS-Typ I) wurden Sonderprogramme entwickelt.
                         Die Programme werden im überarbeiteten Handbuch (Dokument Nr. 13) interpretiert.
                     b. Randmittel werden für Interaktionen auch höherer Ordnung errechnet und ausgegeben
                     c. Programme, die versuchen das Problem der "leeren Zellen" zu lösen, wurden eingefügt.

                     Handbuch:
                     c. Die vier in Almo enthaltenen Schätzverfahren der weighted squares of means (SS-Typ III)
                         der fitting constants I und II (SS-Typ II) und das sequentielle Verfahren (SS-Typ I)
                         werden intensiver behandelt als seither.
                     d. Im Handbuch werden die Randmittel ausführlich erläutert
                     e. Das Problem der "leeren Zellen" wird gründlich diskutiert. Verschiedenen Lösungs-
                         möglichkeiten werden dargestellt und Programme dafür angeboten

 

-------------------------------------------------------------------------------------------------------------
Mit der Version 15 von Almo haben wir aufgehört zu nummerieren, da wir sonst
in den nächsten 85 Jahren (in denen es noch Almo gibt) bei der Version 100
ankommen würden. Wir werden Almo fortwährend verbessern, "verschönern"
und erweitern. Die Änderungen werden jeweils auf der Seite "Download" und
"News" mitgeteilt.
-------------------------------------------------------------------------------------------------------------

 

Änderungen in Version ab Sept. 2017

Wie immer wurden kleine Änderungen vorgenommen, die der Benutzer nicht bemerkt.
Fehler, die dem Benutzer bekannt gemacht werden müssen, haben wir keine entdeckt.

Neu ist folgendes: Prog51m1 zur Wahlhochrechnung und Wählerstromanalyse wurde
überarbeitet. Die Programmeingabe für den Benutzer wurde vereinfacht, die Ergebnisausgabe
übersichtlicher gestaltet und die Grafik teilweise "verschönert". Das Handbuch wurde erheblich
überarbeitet. Nicht nur die Programmeingabe wird erklärt; auch die Methode, die
praktische Vorgehensweise und die Problem des Verfahrens werden ausführlich dargestellt.
Unser Handbuch ist damit eines der wenigen, das die Hochrechnung und Wählerstromanalyse
umfassend darstellt und öffentlich zugänglich ist.
Das Handbuch kann auch separat (ohne das gesamte Almo-Programm) als Dokument 33
herunter geladen werden.

 

Was ist neu in Almo15 ab 1. Sept. 2015

Neu eingeführt wurden die folgenden Verfahren:

    1. die metrische multidimensionale Skalierung (kurz: metrische MDS)
    2. das metrische multidimensionale Unfolding (kurz: metrisches MDU)

Metrische multidimensionale Skalierung (metrische MDS)

An einem Beispiel soll dieses Verfahren kurz vorgestellt werden.
Durch paarweisen Vergleich wurden die Ähnlichkeiten in der Wahrnehmung verschiedener Automarken ermittelt.
Die Kodierungen wurden zu Distanzen (Unähnlichkeiten) "umgedreht". Es entstand folgende Distanzmatrix

                                                     

             Opel VW   Suz  Toy  Merc BMW  Ferr Por  Lamb Roll

Opel         0                                                

VW           3.1  0                                           

Suzuki       5.0  4.4  0                                      

Toyota       3.8  3.3  3.7  0                                  

Mercedes     5.9  5.8  7.0  5.3  0                            

BMW          5.5  5.5  7.0  4.2  2.7  0                       

Ferrari      8.4  8.1  8.3  8.3  6.9  6.8  0                  

Porsche      8.4  8.1  8.4  8.3  6.4  6.4  3.0  0              

Lamborghini  8.5  8.2  8.8  8.7  6.6  6.4  2.1  3.4  0        

Rolls Royce  8.5  8.6  8.9  8.2  5.8  7.0  6.6  6.8  6.3  0   

 

 (Daten aus Internetpaper "Multidimensionale Skalierung", BUGH Wuppertal, 2001                 

 

Almo liefert folgendes Ergebnis:

 

Matrix der Faktorladungen

                      ┌───────────────────────────────┐

                      │  Faktor 1  Faktor 2  Faktor 3 │

 ┌────────────────────┼───────────────────────────────┤

 │Opel        V1      │    3.6170    0.3755   -0.0848 │

 │Volkwage    V2      │    3.5083    0.9681   -0.1096 │

 │Suzuki      V3      │    3.5673    2.1300    2.0885 │

 │Toyota      V4      │    3.7712   -0.2035   -0.1224 │

 │Mercedes    V5      │    0.1811   -2.7555   -1.2839 │

 │BMW         V6      │    0.6122   -1.8120   -2.5856 │

 │Ferrari     V7      │   -4.1109    2.0314    0.0821 │

 │Porsche     V8      │   -3.9372    1.5550   -0.7375 │

 │Lamborgh    V9      │   -4.4048    1.2016   -0.4196 │

 │RollsRoy   V10      │   -2.8042   -3.4905    3.1727 │

 └────────────────────┴───────────────────────────────┘

 

 

Für die 3-Faktoren-Lösung gibt Almo einen Stress von 0.11 und für die 2-Faktoren-Lösung von 0.20 aus.
Der Stress-Koeffizient drückt die Güte einer Lösung aus. Je kleiner der Koeffizient umso besser die Lösung.
Selbstverständlich ist dieses Gütemaß umso besser je mehr Faktoren extrahiert werden.
Nach gängiger Meinung bedeutet ein Stress von 0.20, dass eine ausreichend gute Lösung gefunden wurde.
Es genügt also, 2 Faktoren zu extrahieren.

 

 

Die 3-Faktoren Lösung grafisch dargestellt:

 

 

 

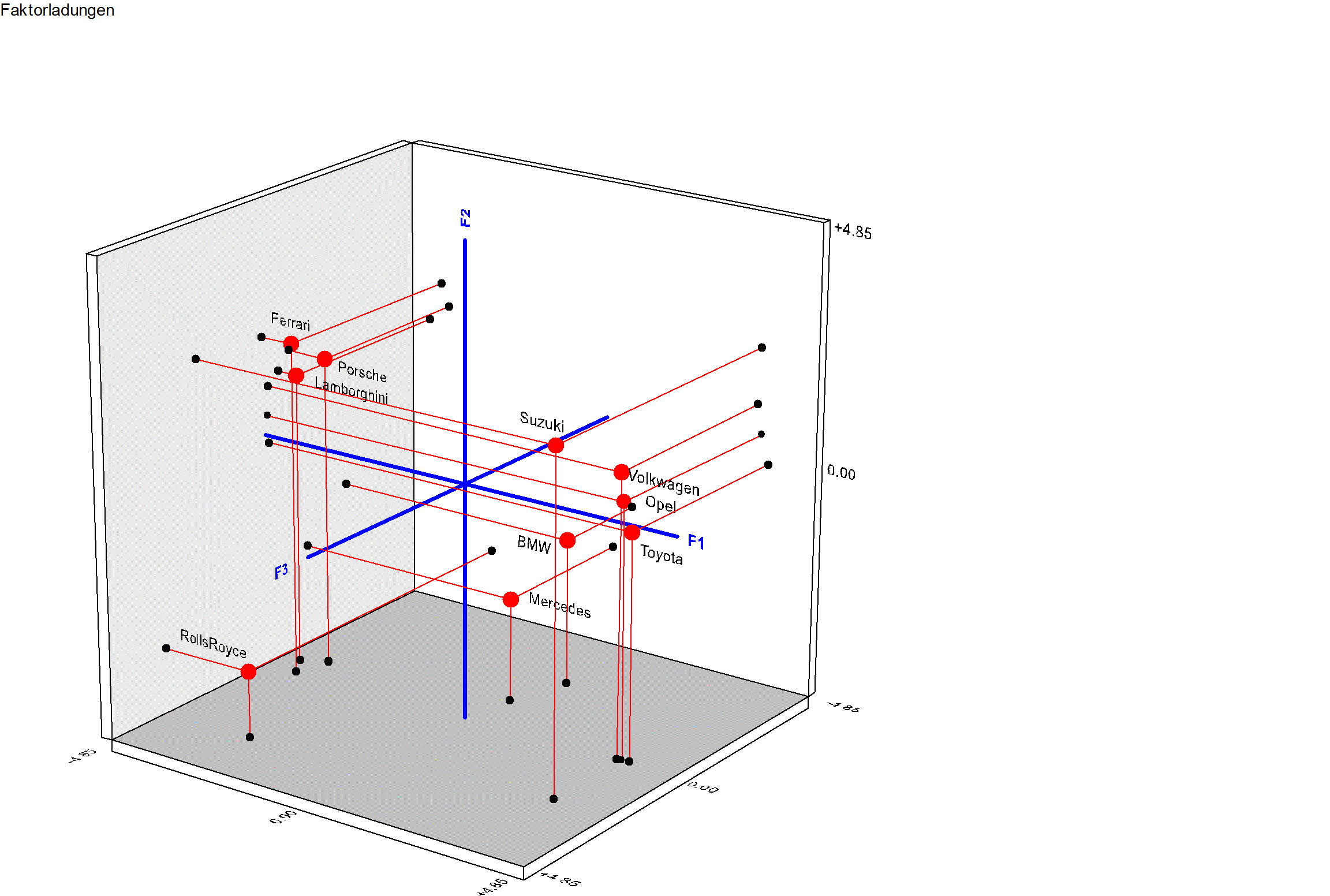
Wir können nun eine Definition der metrischen MDS geben:

 

             Ihre Aufgabe ist es, die Distanzen bzw. Ähnlichkeiten zwischen Objekten in einem
             ein- oder mehrdimensionalen Raum abzubilden.

 

 

 

Das metrische multidimensionale Unfolding (MDU)
An einem Beispiel soll dieses Verfahren kurz vorgestellt werden.
Betrachten wir ein Beispiel. Eine Stichprobe von Personen wird darüber befragt, wie sympathisch sie

 die 5 Parteien ParteiA bis ParteiE finden. Die Personen werden nach Geschlecht und 4 Bildungsstufen

 in 8 Gruppen zusammengefasst. Für jede Gruppe wird der Mittelwert ihrer Sympathie gegenüber den 5 Parteien ermittelt.

Die MDU verlangt, dass Distanzen und nicht Präferenzen bzw. Sympathien als Daten in ihren Kalkül eingegeben werden.
Die Sympathien gegenüber den Parteien wurden mit 1 bis 9 gemessen. Sie werden nun sehr einfach in Distanzen
umgewandelt, indem sie "umgedreht", d.h. von 9 subtrahiert werden

So entsteht folgende Distanzmatrix D

 

                              | Personen-

              Partei          |  Gruppe

      A    B    C    D    E   |    PG

      V1   V2   V3   V4   V5  |    V6

     ---  ---  ---  ---  ---  |  -----

     4.0  3.0  3.0  4.0  6.0  |    1

     3.0  9.0  9.0  2.0  4.0  |    2

     3.0  5.0  6.0  4.0  2.0  |    3

     2.0  4.0  4.0  3.0  3.0  |    4

     4.0  2.0  3.0  5.0  5.0  |    5

     4.0  1.0  2.0  5.0  5.0  |    6

     3.0  9.0  9.0  3.0  2.0  |    7

     4.0  6.0  7.0  4.0  2.0  |    8

 

 

Für obige Distanzmatrix liefert Almo folgende Ladungsmatrix

 

                 Faktor 1   Faktor 2  

         PartA    -1.4382    -0.9737

         PartB     4.5376     0.2255

         PartC     4.5017    -0.9314

         PartD    -2.0639    -1.5698

         PartE    -2.5055     1.2202

      Person-1     2.1970    -2.5389

      Person-2    -4.3112    -2.3061

      Person-3    -0.4993     2.4875

      Person-4     0.4525     0.1589

      Person-5     2.3104     0.6234

      Person-6     2.6130     0.5715

      Person-7    -4.5262     0.2137

      Person-8    -1.2678     2.8193

 

Ähnlich der Faktorenanalyse erhält man eine Ladungsmatrix,
die dann noch grafisch als 2-dimensionales Koordinatensystem dargestellt wird

 

 

 

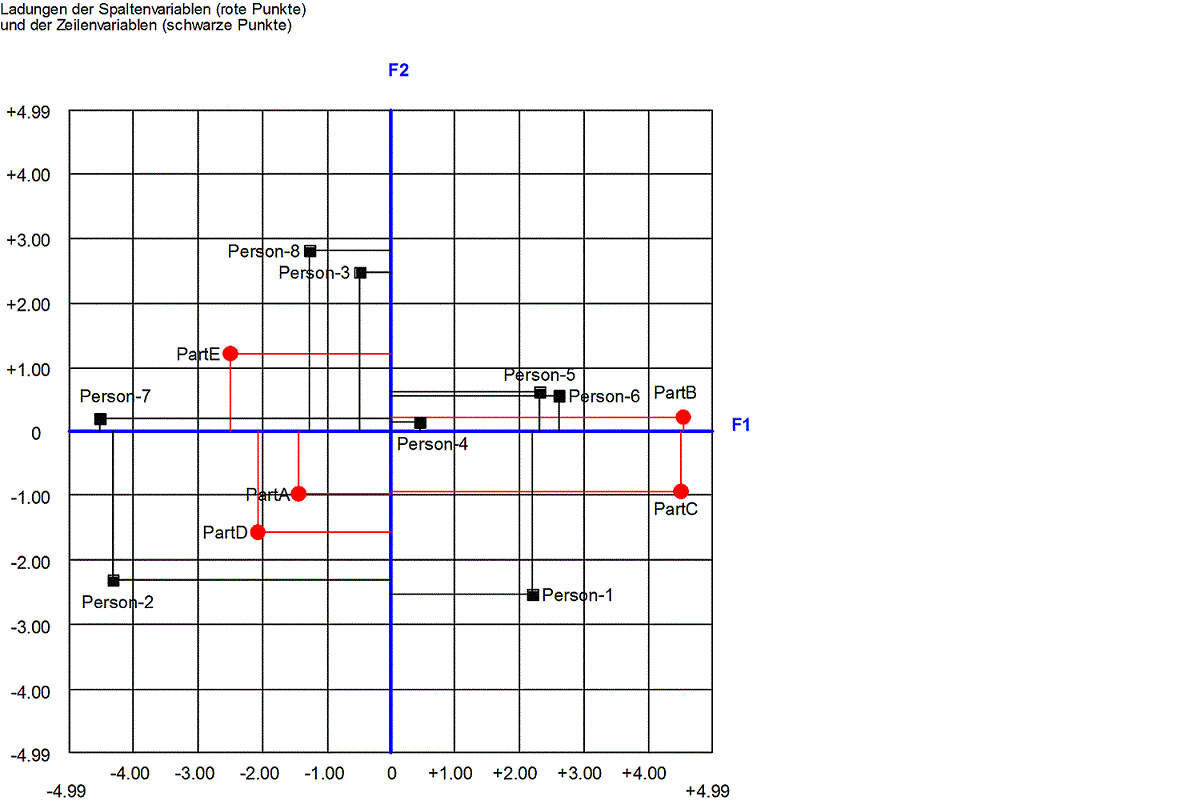
Die Distanz-Urteile der 8 Personengruppen gegenüber den 5 Parteien lassen sich also in 2 Dimensionen arithmetisch
und grafisch darstellen.  Das ist Sinn und Zweck der MDU.
Wir können z.B. erkennen, dass die Personengruppe 1 (etwa junge, hochgebildete Personen) eine große Distanz zur
Partei E haben. Am dichtesten liegen sie bei Partei C. Informationen dieser Art sind natürlich auch aus der Distanzmatrix ablesbar.
Durch die grafische Darstellung werden sie jedoch veranschaulicht. Außerdem leistet die MDU (vergleichbar der Faktorenanalyse)
eine dimensionale Datenreduktion. In der Regel, aber nicht immer, sind die gefundenen Dimensionen inhaltlich benennbar.
In unserem Beispiel könnte vielleicht die eine Dimension als die "Links-Rechts-Dimension" und die zweite als
geographische Nord-Süd-Dimension bezeichnet werden.

Die Leistung der MDU geht aber noch weiter. Aus der Grafik werden auch die Distanzen zwischen den Parteien ersichtlich
und auch zwischen den Personengruppen. So erkennt man z.B. dass Partei C und E am weitesten voneinander entfernt sind.
Bei den Personen sieht man, dass Person-1 und Person-8 am weitesten voneinander entfernt sind.
Das sind Informationen, die aus der Distanzmatrix nicht unmittelbar ersichtlich werden.

 

Was ist neu in Almo ab 1. Sept. 2013 ?
Wieder wurden viele kleine Verbesserungen vorgenommen, von denen der Benutzer
wenig bemerken wird.

Mit großem rechnerischem und programmiertechnischem Aufwand haben wir

                 das allgemeine ordinale Rasch-Modell
                     ("partial credit model")

für dichotome und ordinal-polytome Items in Almo eingefügt. In einer Analyse
dürfen Items mit unterschiedlich vielen und beliebig vielen Ausprägungen vorhanden
sein. Neben vielen Grafiken waren wir darauf bedacht, dem Benutzer "Itemfit-Maße"
anzubieten, die es ihm ermöglichen "nicht-Rasch-konforme" Items zu erkennen.

Der Benutzer findet das neue Programm mit
       Klick auf den Knopf "Verfahren"
       dann "Rasch-Modell" selektieren

Das Handbuch "Das allgemeine ordinale Rasch-Modell" ist im
Almo-Ordner "Handbuch" enthalten. Eine immer wieder aktualisierte
Version kann als separates Almo-Dokument herunter geladen werden.

Alle Unterprogramme sind im Quelltext in der Sprache C und R vorhanden
und dürfen von interessierten Programmierern frei verwendet werden.
Der Benutzer findet sie im Almo-Unterordner "Algorithmen_in_C" im Modul
up_algorith11.c und im Almo-Unterordner "Rasch_in_R"

- Was ist neu in der Version 15 von Almo ?
- Was ist neu in der Version 14 von Almo ?
- Was ist neu in der Version 13 von Almo ?
- Was ist neu in der Version 12 von Almo ?
- Was ist neu in der Version 11 von Almo ?
- Was ist neu in der Version 10 von Almo ?
- Was ist neu in der Version  9 von Almo ?
- Die Koeffizienten der Logitanalyse

Was ist neu in der Version 15 (1. Sept. 2012) von Almo ?

Die Speicherverwaltung des Almo-Editors und der Almo-Oberfläche wurde verändert.

Gelegentliche Abstürze von Almo werden dadurch seltener. In den meisten Fällen

wird ein Absturz dadurch verursacht, dass der Benutzer in die Eingabemasken von

Almo eine unzulässige Eingabe vornimmt - die nicht durch eine der vielen Almo-

Fehlermeldungen abgefangen wird.

 

Bei den "Algorithmen_in_C" wurden die C-Quelltexte eingefügt für:

 

   1. Prog_21: Konfirmatorische Faktorenanalyse mit Eingabe einer fertigen Faktorladungsmatrix
   2. Prog_22: Faktorwerte für die Untersuchungsobjekte berechnen und in eine neue Datei speichern
   3. Prog_23: Rasch-Skalierung
   4. Für alle Programme wurde die Möglichkeit eingebaut, Variablenwerte nach dem Einlesen     

      und vor der Auswerung umzukodieren. In Prog_0.alm wurde diese Möglichkeit exemplarisch
      eingefügt. Siehe "Info5_Umkodier.txt" im Almo-Ordner "Algorithmen_in_C"

 

Besonders interessant dürfte das Rasch-Skalierungs-Verfahren für diejenigen
Benutzer sein, die mit den Pisa-Daten 2012 rechnen wollen. Die Leistungstests zu
Mathematik, Lesen etc. können dann auf ihre Brauchbarkeit für das jeweilige Land
überprüft werden. Die Daten zu Pisa 2012 werden wir im Almo-Format zur Verfügung
stellen, sobald sie vorliegen.

Was ist neu in der Version 14 von Almo ?

Wieder wurden viele kleine Verbesserungen vorgenommen, von denen der Benutzer

wenig bemerken wird.

Neu eingefügt wurde die Konfirmatorische Faktorenanalyse.

 

Bei der konfirmatorischen Faktorenanalyse wird (1) eine aus der Theorie begründete Faktorladungsmatrix

mit (2) einer aus den empirischen Datem gewonnenen Faktorladungsmatrix verglichen und versucht

(3) eine dritte Faktorladungsmatrix als "Kompromiss" zu gewinnen.

Wir bezeichnen die in (1) genannte theoretische Matrix auch als "Zielmatrix", die in (2)

genannte Matrix als "empirische Matrix" und die in (3) genannte Matrix als "konfirmatorische

Matrix".

 

Für die Gewinnung der "konfirmatorischen Faktorladungsmatrix" gibt es 2 Ansätze:

Die Kleinste-Quadrate-Lösung und die Maximun-Likelihood-Lösung.

In Almo ist die Kleinste-Quadrate-Lösung enthalten.

  

Eine bedeutsame Unterscheidung ist die zwischen (1) orthogonaler und (2) schiefwinkliger konfirmatorischer Faktorenanalyse.
Bei ersterer wird angenommen, dass eine orthogonale Lösung den empirischen Daten am besten entspricht
bzw. dass eine aus der Theorie begründete orthogonale Faktorladungsmatrix vorliegt.
Bei der zweiten wird angenommen, dass die Faktoren miteinander korrelieren bzw. dass eine aus
der Theorie begründete schiefwinklige Faktorladungsmatrix vorliegt.

 

Almo enthält zur konfirmatorischen Faktorenanalyse die beiden Programme Pro30m8 und Prog30m9.
Der Benutzer gelangt zu diesen Programmen durch Klick auf den Knopf „Verfahren“ und dann „Faktorenanalyse“.
Ausserdem sind noch 3 Beispielprogramme, die aus Prog30m8 gestartet werden können, vorhanden.

 

Das in Almo realisierte Verfahren kann auch für den Vergleich zweier empirischen Faktorladungsmatrizen

verwendet werden. Beispielsweise könnten die faktorisierten Leistungen von Männern und Frauen in

verschiedenen Tests aufeinder bezogen werden. In diesem Fall liefert das Verfahren
eine dritte Faktorladungsmatrix, die daraus entstand, dass die "Männer-Matrix" maximal an die Frauen-Matrix

"heranrotiert" wurde. Umgekehrt könnte auch die Frauen-Matrix an die Männer-Matrix heranrotiert werden.

Das Ergebnis muss nicht dasselbe sein.

 

Die konfirmatorische Faktorenanalyse wurde auch in die Statistischen Algorithmen in C aufgenommen.
Im C-Modul "a_up_algorith4.c" wurde die Prozedur "a_konfirmator_faktanalyse" und einige zusätzliche

Unterprogramme eingefügt. Wenn der Benutzer die exe-Datei "Prog_20.exe" startet, dann wird
die Eingabe-Datei Prog_20.alm eingelesen und eine konfirmatorische Faktorenanalyse gerechnet.
Das Ergebnis ist dann in Prog_20.erg enthalten.
Die genannten Dateien sind im Ordner ".\Almo14\Algorithmen_in_C\Algorith_Konsole" enthalten.