Folgende Verfahren sind in ALMO enthalten:

1. Häufigkeitsverteilung
2. Basis-Statistiken
3. Nichtparametrische Verfahren
4. Zwei- und drei-dimensionale Tabellierung
5. Beliebig-dimensionale Tabellierung (multidimensionale Kontigenz- und Mittelwertstabellen)
6. Tests auf Differenzen zwischen Variablen
7. Korrelationsmatrix
8. Allgemeines lineares Modell (Regressions-, Varianz- und Kovarianzanalyse, Logit- und Probitanalyse )
9. Kanonische Korrelation
10. Kanonische Diskriminanzanalyse
11. Klassifikation
12. Korrespondenzanalyse
13. Zeitreihenanalyse
14. Pfadanalyse
15. Faktorenanalyse
16. Faktorwert-Ermittlung
17. Clusteranalyse
18. Ähnlichkeits-Skalierung
19. Metrische multidimensionale Skalierung (MDS)
      Metrisches multidimensionales Unfolding (MDU)
      Nicht-metrische multidimensionale Skalierung nach Kruskal
20. Guttman- und Mokken-Skalierung
21. Rasch-Skalierungsverfahren und probabilistisches Unfolding
22. Latente Strukturanalyse nach Lazarsfeld
23. Wählerstromanalyse
24. Soziometrie
25. Zuverlässigkeitskoeffizienten
26. Matrixoperationen
27. Sortieren
28. Ereignisanalyse
29. Conjoint-Analyse (Analyse verbundener Messungen)
30. Nichtlineare Regression mit einer unabhängigen Variablen
31. Datei-Operationen
32. Daten-Import und -Export
33. Zusatzprogramm: Wahl-Hochrechnung
34. Data Mining
35. Datenfusion 
36. Daten-Imputation un3d "plausible values" 
37. Logit und Probit-Analyse (mit Bootstrap)
37. Bootstrap

1. Häufigkeitsverteilung

Ausgezählt werden können Variable mit ganzzahligen Werten, aber auch Variable mit (unbekannten) Dezimalwerten. Neben der Häufigkeitsverteilung werden über Optionen ermittelt. a. Die Vertrauensintervalle (dabei wird das genauere Binomialverteilungsmodell verwendet).

b. Arithmetisches, harmonisches, geometrisches Mittel, Median, 1. und 3. Quartil, Standardfehler des arithmetischen Mittels.

c. Bei ganzzahligen Variablen: Chi-Quadrat-Anpassungstest für Normalverteilung und Gleichverteilung. Schiefe und Exzeß der Normalverteilung.

d. Bei Variablen mit Dezimalwerten: Kolmogorov-Smirnov-Einstichprobentest zur Überprüfung der Normalverteilung oder Gleichverteilung.

e. Binomialtest.

f. Transformation der Daten auf Normalverteilung oder zu Prozentrangwerten.
 

 Schon ausgezählte Verteilungen (etwa aus Statistik-Büchern) können eingeben werden, um für sie die verschiedenen Koeffizienten zu erhalten, die das Programm rechnet.

Die in der Unfrageforschung häufigen Fragen mit Mehrfach-Antworten können ausgezählt werden.
Beispiel: Die Frage "Welche Zeitungen lesen Sie ?", bei der der Befragte mehrere Zeitungen angeben kann, wird ausgezählt.

Die Häufigkeits-Tabellen können durch einen Klick auf einen Knopf als 2D- oder 3D-Balkendiagramme oder als 2D- oder 3D-Liniendiagramme ausgegeben werden.

Beispiel:
Personen wurden nach ihrem Beruf ausgezählt. Das Zählergebnis wird als
Balkendiagramm dargestelt.


 

2. Basis-Statistiken

Das sind Werte-Untergrenzen, -Obergrenzen, Mittelwerte, Standardabweichungen usw.
 

3. Nichtparametrische Verfahren

a. H-Test nach Kruskal-Wallis. Zusätzlich werden die Kontraste zwischen den Rangmittelwerten der verschiedenen Gruppen ermittelt (Test nach Dunn). Bindungen werden nach dem Rangverteilungsverfahren behandelt. Sie werden bei der Berechnung der Testwerte berücksichtigt. Diese Behandlung der Bindungen gilt auch für alle im folgenden beschriebenen Verfahren.

b. U-Test nach Mann-Whitney (bzw. der äquivalente Wilcoxon Rangsummentest). Neben dem üblichen normalapproximierten Test kann für kleine Stichproben der exakte Test gerechnet werden. Dabei kann, im Prinzip, die Stichprobengröße n beliebig groß sein. Allerdings strebt die Rechenzeit für große n gegen unendlich. ALMO berechnet den exakten Test deswegen automatisch nur bis zu einer bestimmten Größe von n. Über eine Option kann diese Schranke höher gesetzt werden. In dieser Weise wird der exakte Test auch bei den Verfahren c bis h gehandhabt.

c. X-Test nach van der Waerden. Asymptotischer und exakter Test

d. Siegel-Tukey-Test für Variabilitätsunterschiede. Asymptotischer und exakter Test.

e. Mood-Test für Variabilitätsunterschiede. Mit exaktem Test.

f. Wilcoxon-Vorzeichenrangtest. Asymptotischer und exakter Test. Neben den Bindungen werden auch die Nulldifferenzen berücksichtigt. Bei größeren Stichproben wird das Cureton-Verfahren angewendet. Bei kleineren Stichproben wird ein exakter Test als Teilrang-Randomisierungstest nach Pratt gerechnet. Das Problem der Bindungen und Nulldifferenzen ist in ALMO somit optimal gelöst.

g. Wilcoxon Vorzeichenrangtest für einen vorgegebenen Median.

h. Shorak-Test für Variabilitätsunterschiede zwischen abhängigen Stichproben. Asymptotischer und exakter Test.

i. Friedman-Test. Zusätzlich berechnet wird der Kendall'sche Konkordanzkoeffizient W und die Kontraste zwischen den Variablen (Meßwiederholungen) nach dem Verfahren von Dunn- Rankin.

j. Vorzeichentest. Er entspricht dem Friedman-Test für nur 2 Variable (Meßwiederholungen).

k. Q-Test nach Cochran. Auch er entspricht dem Friedman-Test für 0-1 kodierte Variable.

 Weitere nicht-parametrische Verfahren sind in anderen Programmteilen von Almo enthalten.
 
 

4. Zwei- und drei-dimensionale Tabellierung

Es können ganzzahlige Variable tabelliert werden, aber auch Variable, die unbekannt viele Dezimalwerte besitzen

          a. Almo erzeugt 2-dimensionale Tabellen folgender Art:

             

b. Drei-dimensionale Tabellen werden erstellt, wobei unter der 3. Variablen 2-dimensionale Partialtabellen gebildet werden. Für diese Partialtabellen können alle die Koeffizienten berechnet werden,
die im Programm angeboten werden. Beispiel für 2 Partialtebellen:

           

c. Der klassische Chi-Quadrat-Test für 2-dimensionale Tabellen wird gerechnet.

d. Korrelationskoeffizienten für nominale Variable
    1. Kontingenzkoeffizient C
    2. Tschuprows T
    3. Cramers V 
    4. Lambda
    5. Vierfelderkorrelation Phi

e. Korrelationskoeffizienten für ordinale Variable
    1. Gamma 
    2. Kendalls tau-b
    3. Spearmans Rho

f. Korrelationskoeffizienten für quantitative Variable
    1. Produkt-Moment-Korrelation r
    2. punktbiseriale Korrelation r(p.bis), eine Variable dichotom andere Variable quantitativ
    3. Eta (eine Variable nominal, andere Variable quantitativ)

g. Ridits, Signifikanz der paarweisen Riditdifferenzen

h. Test für verbundene Stichproben (z.B. Meßwiederholungen)
    1. t-Test 
    2. Wilcoxon Vorzeichenrangtest
    3. Zeichentest
    4. McNemar-Test, Bowker-Test

i. Exakter Fisher-Test. Er wird für schwach besetzte 2*2 Tabellen verwendet (wenn Erwartungswerte kleiner 5 auftreten).

j. Exakter Freeman-Halton-Test für schwach besetzte Tabellen, die größer als 2*2 sind. Dieser Test ist    sehr rechenintensiv.

k. Haldane-Dawson-Test für sehr große, aber schwach besetzte Tabellen 
    (mit Erwartungswerten kleiner 5).

l. Konfigurationsfrequenzanalyse für 2-dimensionale Tabellen mit exaktem Binomialtest (mit     unbeschränkten Zellenhäufigkeiten).

m. Ulemans exakter Rangaufteilungs U-Test. Dies ist ein exakter U-Test für gruppierte Daten mit vielen   Bindungen. Der Test ist sehr rechenintensiv.

n. Kappa-Koeffizient der Urteilsübereinstimmung.

0. tetrachorische und polychorische Korrelation

 Schon ausgezählte Tabellen (etwa aus Statistik-Büchern) können eingegeben werden - um Koeffizienten für sie zu berechnen.

Die in der Unfrageforschung häufigen Fragen mit Mehrfach-Antworten können tabelliert werden.
Beispiel: Die Frage "Welche Zeitungen lesen Sie ?", bei der der Befragte mehrere Zeitungen angeben kann,
wird 2-dimensional tabelliert mit dem Geschlecht des Befragten.

Grafik: 2D- oder 3D-Balken- oder Liniendiagramme

Beispiel:
Das Schulbildungsniveau wird mit dem Beruf tabelliert und durch ein Balkendiagramm graphisch veranschaulicht


 

5. Beliebig-dimensionale Tabellierung

a. Zweidimensionale Mehrfachtabellen. Diese entstehen dadurch, daß verschiedene unabhängige Variable jeweils gegen dieselbe abhängige Variable tabelliert werden. Beispiel:

Die Zahl der Zeilenvariablen ist nicht begrenzt.

b. Partial- bzw. Interaktions-Tabellen. Die Interaktion mehrerer Variablen wird als unabhängige Variable betrachtet, die gegen eine abhängige Variable tabelliert wird. Beispiel:

In diesem Beispiel kann die 1. Teiltabelle als Partialtabelle betrachtet werden. Sie bildet den Zusammenhang zwischen Beruf und Schulbildung für Männer die in der Stadt leben ab.
Die Zahl der interagierenden Zeilenvariablen ist nicht begrenzt.

c. Beliebig-dimensionale Kontingenztabellen mit:

1. Chi-Quadrat-Test auf allseitige Abhängigkeit der an der Kontingenztabelle beteiligten Variablen.

2. 2I-Testt auf allseitige Abhängigkeit

3. Multidimensionale Konfigurationsfrequenzanalyse mit exaktem Binomialtest (mit beliebig großen Zellenhäufigkeiten)

 

       d. Beliebig-dimensionale Mittelwertstabellen:
              Beispiel
              Für Männer und Frauen in den 3 Berufsgruppen Arbeiter,
              Angestellter, Selbständiger wird das mittlere Einkommen und die
              mittlere Leistung in einem Test ermittelt.

 

Schon ausgezählte Tabellen können auch eingegeben werden.

Grafik: 2D- oder 3D-Balken- oder Liniendiagramme
 

6. Tests auf Differenzen zwischen Variablen

a. t-Test für Mittelwertsdifferenz quantitativer Variabler. Zusätzlich der t-Test nach Welch für den Fall der Varianzheterogenität.

b. t-Test für einen (hypothetischen) Mittelwert.

c. t-Test für abhängige Stichproben.

d. Test auf signifikante Ridit-Differenz zwischen ordinalen Var.

e. Median-Test für ordinale Variable

f. Vorzeichentest

g. Verschiedene Tests auf Varianzheterogenität für den uni- und multivariaten Fall: F_max, F_min, Harrison-McCabe, Box-Bartlett
 

 Grafik: 2D- oder 3D-Balken- oder Liniendiagramme

Beispiel:
Die Mittelwerte von Leistung und Einkommen von mehreren Personen werden je Beruf 
durch ein Liniendiagramm dargestellt


 

7. Korrelationsmatrix

Auch Kovarianz- und Quadratsummen-Matrix. Matrix partieller Korrelationskoeffizienten. Einbeziehung von ordinal gemessenen Variablen (tau-b), sowie von nominalen Variablen (Dummy-Variablen) und deren Interaktionen.

In Abhängigkeit vom Messniveau der Variablen x und y werden als PRE-Koeffizienten berechnet:
 
x\y
dichotom

polytom

ordinal
quantitativ
dichotom

Phi

Phi'

biseriales tau-b

punktbiseriales r

polytom

 

Cramer's V

Groß-Gamma

Eta

ordinal
    

tau-b

Groß-Gamma
quantitativ
      

Produkt-Moment r
 
Nominale Variable werden in "Dummies" aufgelöst. Das bedeutet: Eine nominale Variable wird in ihre Ausprägungen aufgelöst. Diese
werden dann als 0, 1 kodierte "nominal-dichotome" Variable behandelt. Sind nominale Variable vorhanden dann berechnet Almo eine
2. Korrelationsmatrix. Dabei werden die Dummies der nominalen Variablen über eine kanonische Korrelationsanalyse zusamengefasst.
Alle (quadrierten) Korrelationskoeffizienten zwischen x und y sind "proportional reduction of error"-Koeffizienten (PRE-Koeffizienten)

Zusätzlich kann auch eine Matrix partieller Korrelationen gebildet werden

Durch Bootstrapping können verteilungsfreie Schätzer für den Standardfehler, den p-Wert und das Konfidenzintervall
für jeden Korrelationskeffizienten  ermittelt werden

Grafik: 3D-Balkendiagramme
Eine von Almo errechnete Korrelationsmatrix kann als Balkendiagramm ausgegeben werden.
Der Benutzer muss nur auf einen Knopf klicken. Almo erzeugt die Grafik dann automatisch.
Die Grafik wird "messerscharf" dargestellt und behält auch beim Ausdrucken ihre Schärfe.
Sie ist deutlich schärfer als nachfolgende Abbildung.

Beispiel:
Die Korrelationen zwischen 4 Variablen werden als Balken dargestellt. In die Grafik ist eine
Nullebene eingezogen. Nach unten gerichtete Balken bedeuten negative Korrelationen

 

8. Allgemeines lineares Modell

a. Regressionsanalyse

b. Varianzanalyse

c. Kovarianzanalyse

d. Diskriminanzanalyse (Schätzung linearer Wahrscheinlichkeiten)

e. Gewichtete Kleinste-Quadrate-Lösung

f. Logit-Analyse, Probit-Analyse. Kleinste-Quadrate-Lösung mit polytomen und ordinalen abhängigen Variablen und nominalen und quantitativen    unabhängigen Variablen. Auch als gewichtete Kleinste-Quadrate-Lösung.

   Als Maximum-Likelihood-Lösung: Binäres, multinominales und ordinales Logit-Modell sowie binäres und ordinales Probit-Modell  (mit Bootstrap)

g. Hierarchische Analysen (variablenweise und gruppenweise)

h. Partielle multiple Bestimmtheitsmaße

i. Analyse von Versuchsplänen mit Meßwiederholungen. Mit univariatem und multivariatem Modell

j. Analyse politischer Wahlen. Aggregatdaten-Analyse

k. Tests auf Homogenität der Varianzen und Regressionen, Linearitätstest

 

- Alle diese Verfahren sind auch als multivariate Analysen mit mehreren (beliebig vielen) abhängigen Variablen rechenbar. 
  Dabei werden Wilks Lambda, Pillais und Hotellings Spur, sowie die zugehörigen F-Werte und Signifikanzen ermittelt.

- Die Zahl der unabhängigen Variablen ist nur durch den Speicher begrenzt.

- Interaktionen beliebiger Ordnung

- Ordinal gemessene Variable können einbezogen werden.

- Nominale Variable als abhängige Variable sind möglich

- Sorgfältige Behandlung fehlender Messwerte. Paarweises oder vollständiges Ausscheiden oder Mittelwerteinsetzung.
   Auch Daten-Imputation möglich. Siehe dazu "Data-Mining".

- Kleinste-Quadrate-Schätzung auch bei ungleichen Zellenhäufigkeiten. Wahlweise durch eines der folgenden Verfahren

a. SS-Typ III (=weighted squares of means)

b. SS-Typ II (=fitting constants)

c. SS-Typ I (=sequentielles Modell)

- Berechnet werden u.a. folgende Koeffizienten: Partielle Regressionskoeffizienten, Korrelationen, Haupt- und Interaktions-Effekte, erklärte   Streuungen, Kontraste,

- jeweils für einzelne unabhängige Variable

- und auch für Variablengruppen

- Prüfung auf lineare Abhängigkeiten zwischen den unabhängigen Variablen (Multikollinearität)

 

Durch Bootstrapping können verteilungsfreie Schätzer für den Standardfehler, den p-Wert und das Konfidenzintervall
für Regressionskoeffizienten der Kovariaten, Haupt- und Interaktions-Effekte, Mittelwertsvergleiche und Randmittel  ermittelt werden
 

 Grafik: 2D- oder 3D- Liniendiagramme, Streudiagramm mit Regressionsgerade, 3D-Streudiagramm mit Regressionsebene. Flußdiagramme für den Zusammenhang zwischen unabhängigen und abhängiger Variablen.

Beispiel:
Die ursächlichen Variablen für die Leistung werden in einem Flußdiagramm veranschaulicht
Auf den einzelnen Richtungsstrecken stehen die Werte der Regressionskoeffizienten bzw. der Effekte


 

9. Kanonische Korrelation

Korrelation zwischen 2 Variablenmengen.Ermittlung der orthogonalen kanonischen Faktoren. Unstandardisierte, standardisierte kanonische Koeffizienten. Kanonische Strukturkoeffizienten. Redundanzanalyse. Kanonische Faktorwerte.

Grafik: 2D- oder 3D-Punkteplots
 

10. Kanonische Diskriminanzanalyse

Ermittlung orthogonaler Diskriminanzfunktionen. Diskriminanzkoeffizienten. Gruppenzentroide. Berechnung von Diskriminanzwerten und Wahrscheinlichkeiten für verschiedene Gruppenzugehörigkeiten.

Grafik: 2D- oder 3D-Punkteplots

Beispiel: 3 Arten von Lilien werden in einem Streudiagramm dargestellt.
Das ist das bekannte Irisbeispiel von R.A. Fisher


 

11. Klassifikation

Ermittelt wird die Wahrscheinlichkeit der Zugehörigkeit zu einer Gruppe, wobei die Gruppenzugehörigkeit unbekannt ist, aber aus einer vorhergehenden Diskriminanzanalyse die Diskriminanzkoeffizienten zur Verfügung stehen.
 

12. Korrespondenzanalyse

Bivariate und multiple Korrespondenzanalyse für beliebig viele nominale Variable. "Supplementary variables". Optimale Skalierung für zwei nominale Variable.

Grafik: 2D- oder 3D-Punkteplots

Beispiel:
Jugendliche wurden befragt, welche Drinks sie drinken, welche Snacks sie essen
und wieviel Geld sie dafür ausgeben. Es lassen sich Typen von Jugendlichen identifizieren.
Beispiel nach Caroll/Green


 

13. Zeitreihenanalyse

Modell 1: Berechnung von gleitenden Durchschnitten und Saisoneffekten. Modell 1 dient (a) der Glättung von Zeitreihen sowie (b) der Zerlegung in eine Trend-, Saison- und eine irreguläre Komponente.

Modell 2: Berechnung von Autokorrelationen und Kreuzkorrelationen sowie von partiellen Autokorrelationen und Kreuzkorrelationen. Modell 2 dient der Identifikation von kausalen Beziehungen zwischen Zeitreihen.

Modell 3: In diesem Modell werden die kausalen Beziehungen zwischen Zeitreihen mit Hilfe regressionsanalytischer Modelle geschätzt. Autokorrelierte Residuen beliebiger Ordnung können berücksichtigt werden.

Grafik: 2D- oder 3D-Liniendiagramme
 

14. Pfadanalyse

Regressionsanalyse rekursiver Kausalmodelle
Grafik: Pfaddiagramm
Betrachten wir ein Beispiel aus der Soziologie: Für 6 Variable wird mit Prog25m1 eine
Pfadanalyse gerechnet. Dabei wird zunächst folgende kausale Reihenfolge angenommen

Herkunft-->Bildung-->Leistung-->Einkommen-->Vermögen-->Konsum

Die Herkunft bestimmt die Bildung, diese die Leistung, ... usw.
Mit Prog25m1 werden die standardisierten Regressionskoeffizienten
für ein volles rekursives Kausalmodell ermittelt. D.h. es wird zunächst
unterstellt, dass in obiger Reihenfolge jede Variable alle
nachfolgenden Variablen determiniert. Danach werden nicht-signifikante
Kausalpfade eliminiert.

Auf den Pfeilen in nachfolgendem Pfaddiagramm stehen die (standardisierten) Regressionskoeffizienten.
Pfeile, deren Regressionskoeffizienten nicht signifikant sind, werden eliminiert.
Signifikante Pfade sind durch 1 oder 2 oder 3 Sterne markiert. 
Standardmäßig werden an den Regressionskoeffizient angehängt:
1 Stern wenn seine Sigifikanz p <= 0.05
2 Stern wenn seine Sigifikanz p <= 0.01
3 Stern wenn seine Sigifikanz p <= 0.001
Im Almo-Grafik-Editor können die Signifikanzen je Stern anders definiert werden.


 15. Faktorenanalyse

a. Hauptachsen-Lösung

b. Hauptkomponenten-Lösung

c. Alpha-Faktorenanalyse

d. Image-Faktorenanalyse

e. kanonische Faktorenanalyse.

f. nominale Faktorenanalyse: Faktorenanalyse mit polytomen nominalen Variablen nach dem Blockdiagonal-Verfahren von McDonald oder durch multiple Korrespondenzanalyse

g. auch Faktorenanalyse der Kovarianzmatrix

h. rechtwinklige Varimax-Rotation

i. schiefwinkliger Quartimin-Rotation

j. Kommunalitäten: 1.0 oder multiple Bestimmtheitsmaße oder maximale Korrelation oder selbst eingegebene Werte
   frei wählbare Zahl von Kommunalitäten-Iterationen

k. Berechnung von Faktorwerten für Untersuchungsobjekte

l. Ermittlung der Faktoren-Signifikanz

m. Konfirmatorische Faktorenanalyse, recht- und schiefwinklig, Kleinste-Quadrate-Lösung, "konfirmatoeische" Faktorwerte
 

 Grafik: 2D- oder 3D- Punkteplots für recht- und schiefwinklige Faktorräume.

Beispiel:
6 Sportarten werden faktorenanalytisch untersucht. Es erweist sich, dass sie auf die 3 Faktoren
Schnelligkeit, Ausdauer und Kraft zurückgeführt werden können

 

16. Faktorwert-Ermittlung

Ermittlung von Faktorwerten mit Abspeichern in eine Datei

 

17. Clusteranalyse

 

A. Hierarchische Verfahren:

a. 
 single linkage
b. 
 complete linkage 
c. 
 average linkage
d. 
 weighted average linkage 
e. 
 median linkage
f. 
 centroid linkage 
g. 
 Ward linkage
h. 
 complete linkage für überlappende Cluster
i. 
 Within-Linkage
j. 
 gegenseitiges Nächste-Nachbarn-Verfahren
 
Es wird eine Fülle von Distanzmaßen berechnet. Zur Überprüfung der Brauchbarkeit einer Clusterlösung können Korrelations- und Homogenitätsmaße sowie Stabilitätswerte mit Hilfe des Rand-Index berechnet werden. Für eine Clusterlösung kann darüber hinaus eine Zufallstestung durchgeführt werden. In einem Programm können mehrere Verfahren mit unterschiedlichen Distanzmaßen gerechnet werden. Zur Behandlung fehlender Werte stehen drei Mödlichkeiten zur Verfügung.

Grafik: Dendrogramme, 2D- oder 3D-Liniendiagramme
Beispiel:




B. K-Means-Clusterverfahren für beliebig viel Objekte.

6 Modelle für das K-Means-Verfahren mit unterschiedlicher Gewichtung der Distanzen. Analyse latenter Profile (nach Lazarsfeld und Henry), probabilistische Clusteranalyse (Analyse latenter Klassen) für Variablen mit beliebigem Messnievau und Repräsentanten-Verfahren. Konfirmatorische Clusteranalysen bei allen Verfahren. 5 Startwertverfahren. Eines davon kann als Quick-Clustering-Methode verwendet werden. Zur Bestimmung der Clusterzahl werden eine Reihe von Maßzahlen (Eta-Quadrat, Pseudo-F-Wert, Bealsche F-Werte und ML- und Chi-Quadrat-Werte bei der probabilistischen Clusteranalyse) berechnet. Die Interpretation der gefundenen Clusterlösung wird dadurch erleichtert, daß das Programm untersucht, in welchen Klassifikationsmerkmalen sich die Cluster signifikant unterscheiden und welche Beziehungen zwischen den Klassifikationsmerkmalen innerhalb der Cluster bestehen. Dazu wird innerhalb jedes Clusters eine hierarchische Clusteranalyse gerechnet.

Grafik: 2D- und 3D-Liniendiagramme
 

Beispiel: Bekleidungs-, Trink- und Rauch-Gewohnheiten von Jugendlichen
              Liniendiagramm der Clustermittelwerte

 
 
Die senkrechte "0.00-Linie" kennzeichnet den Durchschnitts-Jugendlichen.
Betrachten wir Cluster 2 (blaue Linie). Es sind dies Jugendliche, die sich überdurchschnittlich
häufig knonventionell kleiden, stark überdurchschnittlich Bier trinken und leicht über-
durchschnittlich viel rauchen. Sie sind eher männlich und ihr Bildungsgrad ist leicht
unterdurchschnittlich. Geradezu ein Gegentyp dazu bildet Cluster 3 (gelbe Linie). Diese
Jugendlichen kleiden sich elegant, sie trinken eher Wein und rauchen wenig. Sie sind eher
weiblich und ihr Bildungsgrad ist überdurchschnittlich.

C. Mehrstufige Clusteranalyse

2-stufiges Verfahren:
Es wird zuerst eine k-means-Clusteranalyse gerechnet. Dabei werden sehr viele Cluster gebildet. Diese Cluster werden mit ihren Mittelwerten in den Klassifikationsvariablen als Objekte in die 2. Stufe, die hierarchische Clusteranalyse eingelesen. Deren Ergebnisse sind dann die entgültigen Ergebnisse

3-stufiges Verfahren:
Zuerst wird wie beschrieben ein 2-stufiges Verfahren gerechnet. Die Ergebnisse aus der 2. Stufe, der hierarchischen Clusteranalyse, 
werden dann als Startwerte in das k-means-Verfahren eingegeben. Dies ist dann die 3. Stufe der Analyse.

Überspringe Stufe 1:
Fordert der Benutzer ein 3-stufiges Verfahren an und verlangt er, dass Stufe 1 (das k-means-Verfahren) übersprungen wird,
dann führt Almo ein 2-stufiges Verfahren durch, bei dem in der 1. Stufe eine hierarchische Analyse gerechnet wird, deren Ergebnisse
als Startwerte in das k-means-Verfahren eingegeben werden, das somit die abschliessende 2. Stufe bildet

18. Ähnlichkeits-Skalierung

a. Paarvergleich b. Rangordnung

c. Tetradenvergleich d. Tripelvergleich

e. multiple Rangordnung f. Rangordnung von Paaren

g. Image-oder Profil-Analse

 

19. Metrische multidimensionale Skalierung (MDS)
      Nicht-metrische multidimensionale Skalierung nach Kruskal
      Metrisches multidimensionales Unfolding (MDU)

MDS

Analyse der Dimensionen metrischer und nicht-metrischer Objekt-Ähnlichkeiten bzw. -Unähnlichkeiten.
Dimensionale Analyse von Distanzen bzw. Präferenzen von Untersuchungseinheiten gegenüber Objekten.

Grafik: 2D- oder 3D-Punkteplots
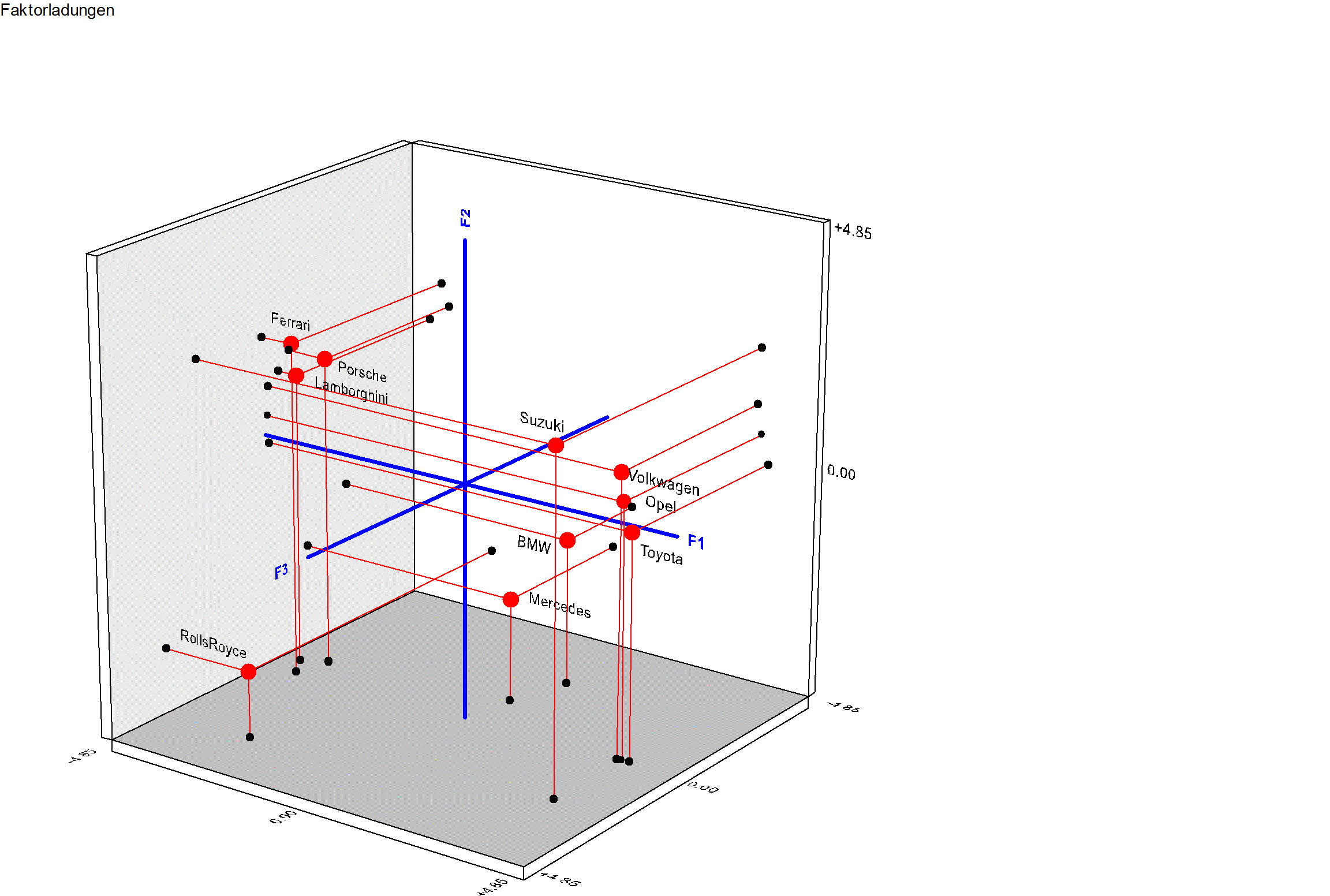
Beispiel: Die Ähnlichkeiten in der Wahrnehmung zwischen verschiedenen Automarken werden
in einer Ähnlichkeitsmatrix dargestellt. Die Matrix wird entweder nach einem metrischen oder
einem iterativen nicht-metrischen Kalkül dimensional zerlegt (faktorisiert). Es entsteht
folgende Ladungsmatrix

                      ┌───────────────────────────────┐
                       │  Faktor 1  Faktor 2  Faktor 3 │

 ┌────────────────────┼───────────────────────────────┤
 │Opel        V1      │    3.6170    0.3755   -0.0848 │
  │Volkwage    V2      │    3.5083    0.9681   -0.1096 │
   Suzuki      V3      │    3.5673    2.1300    2.0885 │
 │Toyota      V4      │    3.7712   -0.2035   -0.1224 │
  │Mercedes    V5      │    0.1811   -2.7555   -1.2839 │
  │BMW         V6      │    0.6122   -1.8120   -2.5856 │
  │Ferrari     V7      │   -4.1109    2.0314    0.0821 │
  │Porsche     V8      │   -3.9372    1.5550   -0.7375 │
  │Lamborgh    V9      │   -4.4048    1.2016   -0.4196 │
  │RollsRoy   V10      │   -2.8042   -3.4905    3.1727 │
  └────────────────────┴───────────────────────────────┘

Diese Ladungsmatrix wird in einem 2- oder 3-diemsionalen Koordinatensystem
abgebildet. Das 3-dimensionale System, ist folgendes

mMDS2d

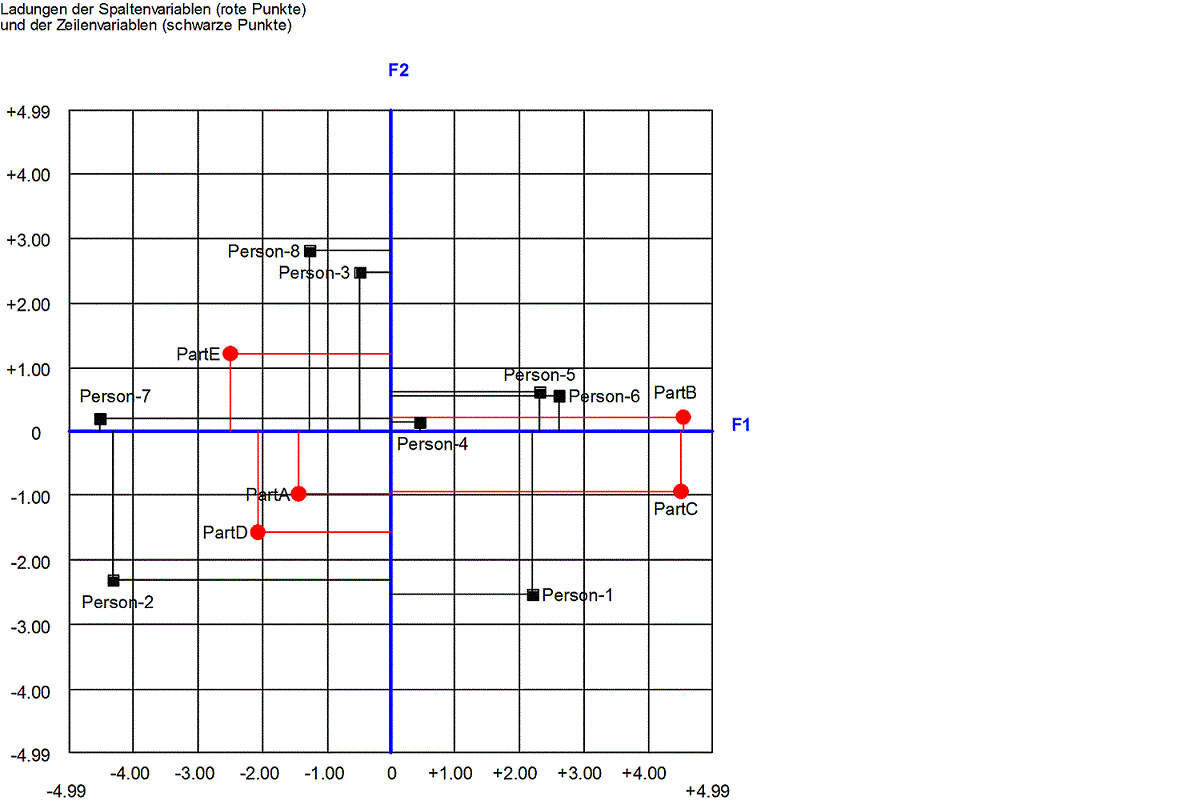
MDU

Beispiel für das metrische multidimensionale "unfolding": Eine Stichprobe von Personen wird darüber befragt,
wie sympathisch sie die 5 Parteien ParteiA bis ParteiE finden. Die Personen werden nach Geschlecht und 4 Bildungsstufen
in 8 Gruppen zusammengefasst. Für jede Gruppe wird der Mittelwert ihrer Sympathie gegenüber den 5 Parteien ermittelt.
Es entsteht folgende Distanzmatrix:

              Partei          |  
       A    B    C    D    E   | Personen-   
       V1   V2   V3   V4   V5  |  Gruppe 
     ---  ---  ---  ---  ---  |  -----
     4.0  3.0  3.0  4.0  6.0  |    1
     3.0  9.0  9.0  2.0  4.0  |    2
     3.0  5.0  6.0  4.0  2.0  |    3
     2.0  4.0  4.0  3.0  3.0  |    4
     4.0  2.0  3.0  5.0  5.0  |    5
     4.0  1.0  2.0  5.0  5.0  |    6
     3.0  9.0  9.0  3.0  2.0  |    7
     4.0  6.0  7.0  4.0  2.0  |    8

Die Distanzmatrix wird nach einem speziellen Verfahren faktorisiert. Es entsteht folgende Ladungsmatrix

                 Faktor 1   Faktor 2  

         PartA    -1.4382    -0.9737

         PartB     4.5376     0.2255

         PartC     4.5017    -0.9314

         PartD    -2.0639    -1.5698

         PartE    -2.5055     1.2202

      Person-1     2.1970    -2.5389

      Person-2    -4.3112    -2.3061

      Person-3    -0.4993     2.4875

      Person-4     0.4525     0.1589

      Person-5     2.3104     0.6234

      Person-6     2.6130     0.5715

      Person-7    -4.5262     0.2137

      Person-8    -1.2678     2.8193

 

    Die Ladungsmatrix wird in folgendem 2-dimensionalen Koordinatensytem abgebildet

metrMDU

Die Distanz (1) zwischen den Personen, (2) zwischen den Parteien und (3) zwischen Personen und Parteien werden ersichtlich

20. Guttman- und Mokken-Skalierung

Skalierung dichotomer und polytomer Items

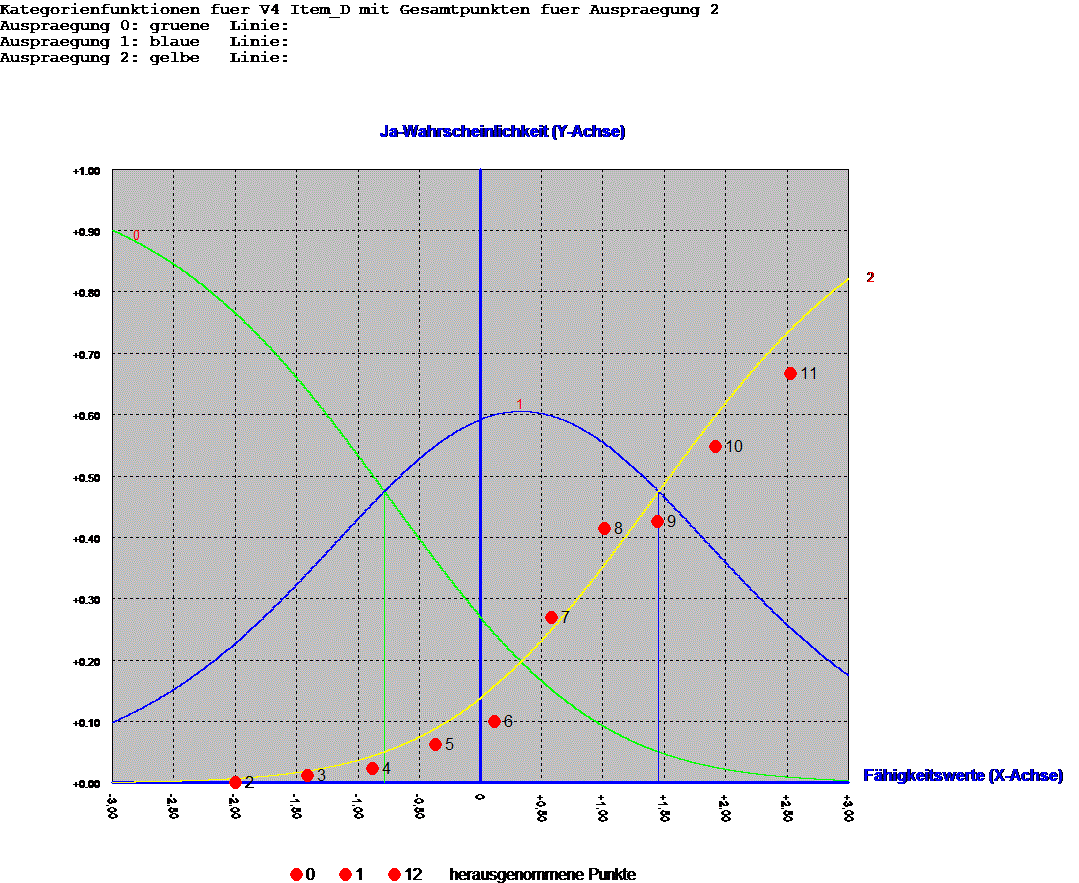
Grafik: Liniendiagramm der "trace-line"

Beispiel:
Personen werden befragt, welche politischen Aktivitäten sie durchführen.
Die tracelines dieser politischen Aktivitäten werden dargestellt


 

21. Dichotome und ordinal-polytome Rasch-Skalierung und probabilistisches Unfolding

Grafik: Liniendiagramm der "trace-line"
Beispiel für dichotomes Item:

dichoRasch

 

Beispiel für Item mit 3 Kategorien

 polyRasch
 

22. Latente Strukturanalyse nach Lazarsfeld

a. Modell mit linearer Itemcharakteristik

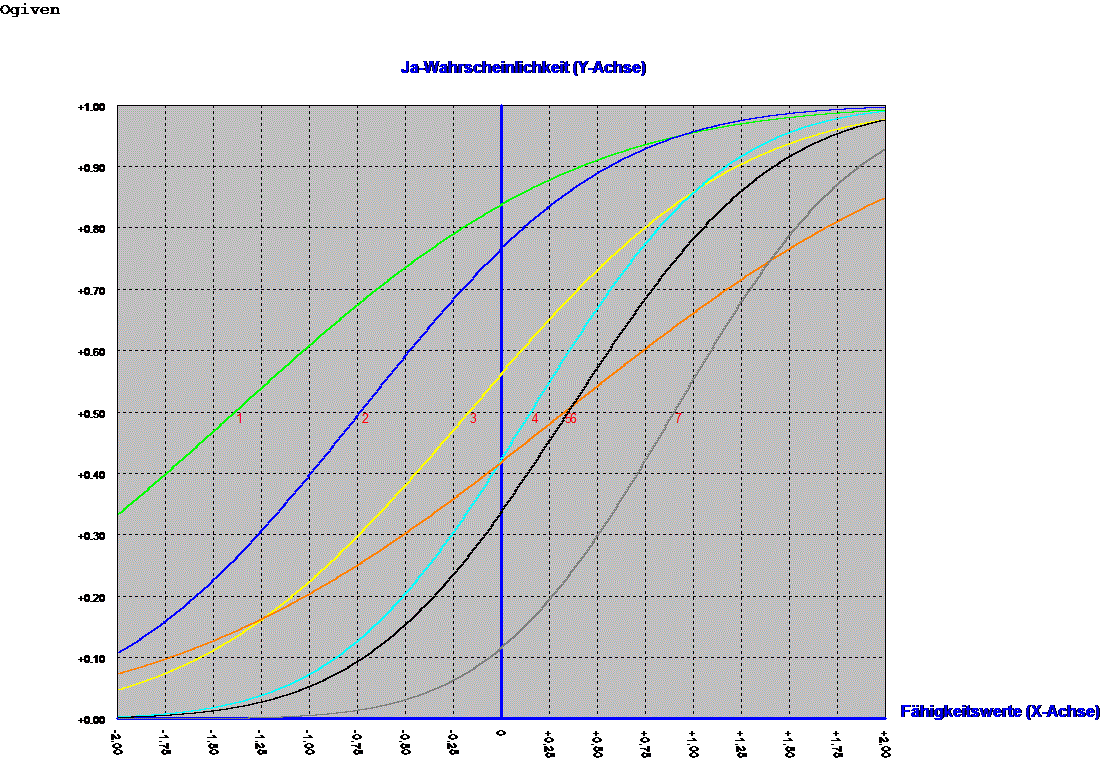
b. Guttman-Skala

c. restringiertes latent-distance-Modell

d. allgemeines latent-distance-Modell

e. Ogiven-Modell (besonders empfehlenswert)

f. latent-class-Modell (nur 2 Klassen)

g. latent-class-Modell (allgemeine Lösung)

 Grafik: Liniendiagramm der "trace-line"
 Beispiel für 7 Items des Ogiven-Modells:

ogive

 

 23.Wählerstrom-Analyse durch Quadratische Optimierung

Grafik: 2D- und 3D-Balken- oder Liniendiagramme für Wählerströme
 

24. Soziometrie

Ergebnisse des soziometrischen Tests (mit positiven und negativen Wahlen, mit fixierter und unbeschränkter Wahlzahl) werden ausgewertet. Soziometrischer Status, Gruppenkohäsion, Cliquenbildung und eine Vielzahl weiterer Koeffizienten werden berechnet. Gruppierungsmerkmale (z.B. Geschlecht) können miteinbezogen werden.
 

25. Zuverlässigkeitskoeffizienten

Berechnet werden Cronbachs Alpha, Spearman-Brown, Guttmans Maß, Armors Theta, Heise u. Bohrnstedts Omega usw.
 

26. Matrixoperationen

Inverse, Determinante, Ermittlung linearer Abhängigkeiten zwischen Variablen
Matrix-Multiplikation, -Transponierung. Erzeugen von Distanzmatrizen aus Ladungsmatrizen
 

27. Sortieren

Sortieren von Dateien nach Zeichen-Variablen oder numerischen Variable. Aufsteigend oder absteigend.
 

28. Ereignisanalyse

Bei der Sterbetafel-Methode und dem Kaplan-Meier-Verfahren werden neben der Überlebensfunktion eine Fülle weiterer Koeffizienten berechnet. Bei beiden Verfahren ist es möglich die Überlebensfunktion verschiedener Gruppen (z.B. von Arbeitern, Angestellten, Bauern) auf paarweise signifikante Differenz zu testen. Mit der Cox-Regression werden die Determinanten der Überlebensdauer identifiziert.

Grafik: 2D- und 3D-Liniendiagramme der Überlebensfunktion.
Beispiel:


 

29. Conjoint-Analyse (Analyse verbundener Messungen)

Aus Präferenzurteilen von Untersuchungspersonen über Objekte wird auf die relative Wichtigkeit der Merkmale der Objekte geschlossen.

Grafik: 2D- und 3D-Liniendiagramme
 Beispiel:


 

30. Nichtlineare Regression mit einer unabhängigen Variablen

Grafik: Kurven- und Streudiagramme
Beispiel:

  

31. Datei-Operationen

                    a. Anhängen von Datensätzen an bestehende Dateien. b. Bildung von Sub-Dateien

c. Sortieren von Dateien nach String- und/oder numerischen Variablen

d. Zusammenfügen von Dateien in jeglicher Weise, auch über Verbindungsvariable.

e. Relationale Datenbank-Operationen, wie z.B. Suchen über mehrere Dateien mittels Verbindungsvariable.
 

32. Daten-Import und Export

Daten aus SPSS und Excel können in das Almo-Format gewandelt werden - und umgekehrt

33. Zusatzprogramm: Wahl-Hochrechnung

Vollständiges Hochrechnungssystem für Wahlen. Mit Mandatsverteilung. Mit Wählerstromanalyse.. 
Nicht im Standard-Almo enthalten. Fordern Sie bitte Informationen an. Siehe auch Webseite zu Wahlhochrechnung

34. Data Mining

Folge von mehreren Almo-Programmen zur Entdeckung von Zusammenhängen zwischen Variablen und von
Zusammengehörigkeiten von Objekten. Siehe Webseite zu Data Mining

35. Datenfusion

Siehe Webseite zu Data Mining

36. Daten-Imputation und "plausible values"

Mittelwerte oder Mediane oder Erwartungswerte für fehlende Werte einsetzen.
Prognosewerte bzw. "zufallsüberlagerte" Prognosewerte für fehlende Werte einsetzen
     Formen:
        1. singuläre Imputation
        2. multiple Imputation
        3. "plausible values" Imputation

     Verfahren:    
        1. ALM-Imputation: Imputation durch Allgemeines Lineares Modell (ALM)
        2. HALM-Imputation: ALM-Imputation mit vorausgehender Hauptkomponenten-Zerlegung
        3. Logit-Imputation: Imputation durch Logitanalyse
        4. Cluster-Imputation: Imputation durch Clusteranalyse

 Almo enthält folgende 8 Programm-Masken zur Daten-Imputation

                        ALM-          HALM-          Logit-         Cluster-
                        Imputation    Imputation     Imputation     Imputation

┌────────────────────┬─────────────┬──────────────┬──────────────┬──────────────┐
│Ein-Wert-Imputation │ Prog45mm_fw │ Prog45Hk_fw  │   Prog45mz   │ ProgImp_Clust│
│multiple Imputation │ Prog45mm_Imp│ Prog45Hk_Imp │              │              │
│plausible values    │ Prog45mm_PV │ Prog45Hk_PV  │              │              │
│Imputation          │             │              │              │              │
└────────────────────┴─────────────┴──────────────┴──────────────┴──────────────┘

Programm Prog20mo zum ALM wurde so erweitert, dass es Daten, die multipel
imputierte Variable oder "plausible values" enthalten, auswerten kann.

 

37. Bootstrap

In Almo kann gegenwärtig das Bootstrap-Verfahren eingesetzt werden für

              1. die Basisstatistiken mit Programm-Maske Prog05m6
              2. Häufigkeitsverteilung. Anteilswerte mit Bootstrap mit Prog05m7

              3. die Korrelationsmatrix (inkl. Partialmatrix) mit Programm-Maske Prog19em

              4. das Allgemeine Lineare Modell (ALM) mit Programm-Maske Prog20my
              5. Logit- und Probitanalyse mit Programm-Maske Prog22m5
              6. Faktorenanalyse mit Prog 30ml
              7. Korrespondenzanalyse mit Prog30mm

Siehe ausführlichere Darstellung  hier

 

Für das Bootstrap-Verfahren, insbesondere für das Bootstrap beim ALM,
beim Logit- und Probit-Modell und bei der Faktorenanalyse wurden je ein
ausführliches Handbuch verfasst. (hier)          

Almo-Dokument 13b "Bootstrap beim Allgemeinen Linearen Modell"

                              9b "Bootstrap beim Logit- und Probit-Modell"             

                            15a "Bootstrap bei Faktorenanalyse"
                             35 "Konfidenzintervall und p-Wert beim Bootstrap"

Es ist beabsichtigt weitere in Almo vorhandene statistischen Verfahren noch durch Bootstrap zu erweitern.